前言:古希腊毕达哥拉斯学派在研究音调和数字比值之间的关系时发现:一根长为12的弦若变为原来的3/4长,那么音调会比原调高出四度;变为2/3则音调升高五度;变为1/2长则提高八度,即高一个音阶。这里弦的长度分别为12、9、8和6。这里就涉及到了算术平均和调和评论的概念。
平均数分类
我们日常生活和数学统计中常用到平均数一般分为四类:算术平均数、几何平均数、调和平均数、加权平均数。下面分类介绍一下。
1、算术平均数与加权平均数
算术平均数
算术平均数也称均值,是统计学中最常用的指标,在生活中也经常用到。其定义为:若一组数据为:x1、x2、x3…xn,则这组数据的算术平均值为:
x拔=(x1+x2+x3+…xn)/n。
例如:学校学期末考试,假如某数学得了84,语文92,英语91,那么算术平均数就是(84+92+91)/3=89。
算术平均数是最简单的加一种指标,在统计学中,还有一种常用的指标就是加权平均数。简单说就是一组数据中,把每个数据乘于它对应的权重值,再将结果求和即可。它的表达式是:若一组数据为x1、x2、x3…xn,其对应的权重为y1、y2、y3…yk、其中y1+y2+y3+…+yk=n。则加权平均数=(x1y1+x2y2+…+xkyk)/n。算术平均数实际上是各权重相等的加权平均数,是加权平均数的特殊情况。
例如,某人射击十次,其中二次射中10环,三次射中8环,四次射中7环,一次射中9环,那么他平均射中的环数为:
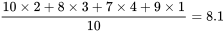
加权平均数
这里,7,8,9,10这四个数是射击者射中的几个不同环数,但它们出现的频数不同,分别为4,3,1,2就称之为权数或权重。假设它们出现的次数都为2.5次(此处为了计算比较,当然现实中不可能出现2.5次这种情况),则上述平均值变为(10x2.5+9x2.5+8x2.5+7x2.5)/10=(10+9+8+7)x2.5/10=(10+9+8+7)/4。即四个数的算术平均数。加权平均在生活中也经常用到,比如考研复试时,最终成绩就是把笔试成绩和面试成绩按一定的权重合成的成绩。大学的期末考试成绩计算同样如此。
2、几何平均数
几何平均数的定义为:若一组数据为x1、x2、x3…xn,则其几何平均值为(x1x2x3…xn)^(1/n)。几何平均数处理的数据一般都为正数。其应用一般都是对比率、指数、利率、发展速度等进行平均。例如一个工厂知道每月的增长率,求年增长率。假定某地储蓄年利率(按复利计算):5%持续1.5年,3%持续2.5年,2.2%持续1年。求此5年内该地平均储蓄年利率。例如,知道某地10年内储蓄年利率(按复利计算)的值和持续年数,求10年内该地平均储蓄年利率。
3、调和平均数
调和平均数又称倒数平均数,它等于各项取倒数后的算术平均数的倒数。若一组数为x1、x2、x3…xn,则调和平均数=1/[(1/x1+1/x2+…+1/xn)/n]。调和平均数可以用在相同距离但速度不同时,平均速度的计算;在电路中求两个电阻R1, R2并联后的等效电阻R等。回到开头提到的弦长问题,长度分别为12、9、8和6的弦对应不同的音调,其中9是12和6的算术平均数。8则是12和6的调和评论数。另外,调和级数的每一项(第一项除外),都是前后两项的调和平均数。
4、三个平均数之间的关系
记算术平均数为S,几何平均数为J,调和平均数为T,则有S≥J≥T。当且仅当数组所有数都相等时等号成立。







