一、三角形全等

1. 全等三角形：两个能够完全重合的三角形叫全等三角形

2. 全等三角形的性质：全等三角形的对应边相等，对应角相等

3. 全等三角形的判定定理：

（1）一般三角形有SAS、ASA、AAS、SSS

（2）直角三角形还有个HL

注意：如果两个三角形具备了“SSA”的条件，不能判定这两个三角形全等。

二、角平分线的性质和判定

1.角平分线上的点到角两边的距离相等

2.角的内部到角两边距离相等的点在角平分线上

三角形全等的判定与性质的综合运用

三、例题讲解

例题2：

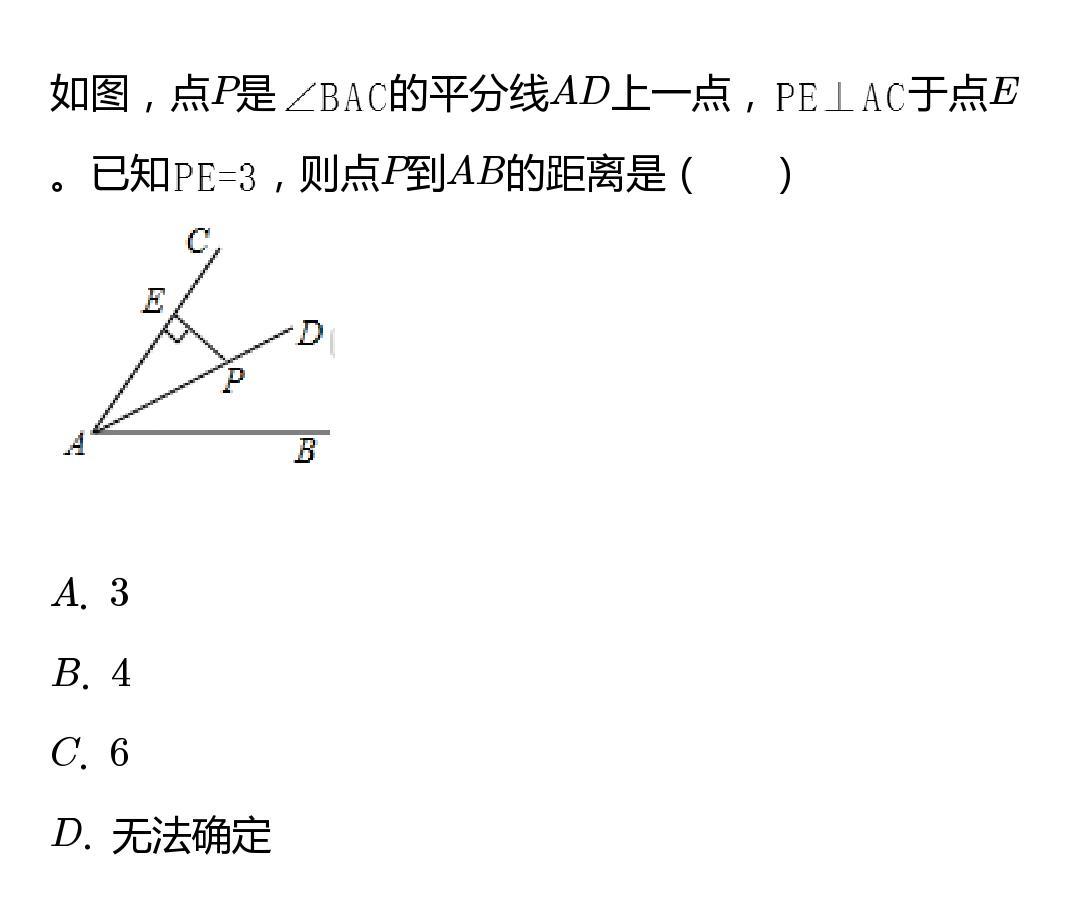
解：这道题目主要考查的是角平分线的性质：角平分线上的点到角两边的距离相等，由点到直线的距离定义可知，PE=3，就是点P到直线AC的距离，而点P在角BAC的平分线上，根据角平分线的性质可知，点P到AB的距离也为3，所以答案选择A

答案：A

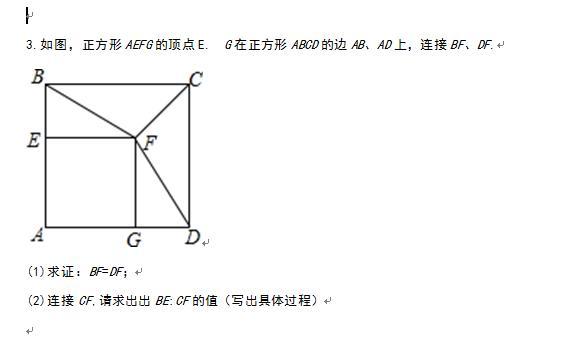
四、总结

1.全等三角形是几何论证的工具，在以后的学习中经常用到，利用全等三角形可以解决线段相等、角相等以及直线平行等问题，经常在各地的考题中出现，需要重点掌握

2.角平分线的性质与判定在三角形全等的证明与应用中有着非常重要的作用，有以下情况：

（1）在证明线段相等或者角相等的问题时，能用角的平分线性质时直接用，若仍去找全等三角形，相当于重新证明了这个结论，所以能用简单的方法时不要绕远路。

（2）有角平分线（或证明角平分线时），常过角平分线上的点向角的两边作垂线段，利用角平分线上的点到角两边的距离相等证明。