1、直线的方向向量和平面的法向量1.直线的方向向量:若A、B是直线上的任意两点,则为直线的一个方向向量;与平行的任意非零向量也是直线的方向向量.2.平面的法向量:若向量所在直线垂直于平面,则称这个向量垂直于平面,记作,如果,那么向量叫做平面的法向量.3.平面的法向量的求法(待定系数):(1)建立适当的坐标系.(2)设平面的法向量为.(3)求出平面内两个不共线向量的坐标.(4)根据法向量定义建立方程组.

(5)解方程组,取其中一组解,即得平面的法向量.
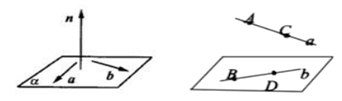
2、用向量方法判定空间中的平行关系1.线线平行:设直线的方向向量分别是,则要证明∥,只需证明∥,即. 即:两直线平行或重合两直线的方向向量共线。2.线面平行(1)设直线的方向向量是,平面的法向量是,则要证明∥,只需证明,即.即:直线与平面平行直线的方向向量与该平面的法向量垂直且直线在平面外(2)要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可.3.面面平行:若平面的法向量为,平面的法向量为,要证∥,只需证∥,即证. 即:两平面平行或重合两平面的法向量共线。3、用向量方法判定空间的垂直关系1.线线垂直:设直线的方向向量分别是,则要证明,只需证明,即. 即:两直线垂直两直线的方向向量垂直。2.线面垂直(1)设直线方向向量是,平面法向量是,则要证明,只需证明∥,即.(2)设直线的方向向量是,平面内的两个相交向量分别为,
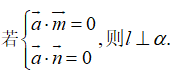
即:直线与平面垂直直线的方向向量与平面的法向量共线直线的方向向量与平面内两条不共线直线的方向向量都垂直。3.面面垂直:若平面的法向量为,平面的法向量为,要证,只需证,即证. 即:两平面垂直两平面的法向量垂直。19.7 空间向量运用:4、利用向量求空间角1.求异面直线所成的角:已知为两异面直线,A,C与B,D分别是上的任意两点,所成的角为,则
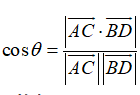
2.求直线和平面所成的角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做该斜线和这个平面所成的角(2)求法:
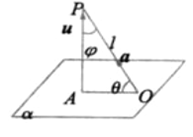
设直线的方向向量为,平面的法向量为,直线与平面所成的角为,与的夹角为,则为的余角或的补角的余角.即有:
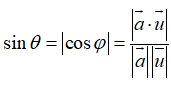
3.求二面角的平面角(1)定义:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面
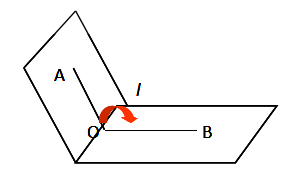
二面角的平面角是指在二面角的棱上任取一点O,分别在两个半平面内作射线,则为二面角的平面角.(2)求法:设二面角的两个半平面的法向量分别为,再设的夹角为,二面角的平面角为,则二面角的平面角为的夹角或其补角根据具体图形确定是锐角或是钝角:如果是锐角,
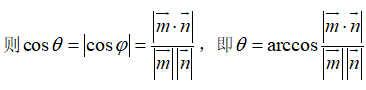
如果是钝角,
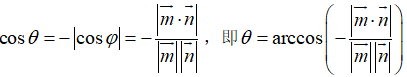
5、利用法向量求空间距离1.点到直线距离:若Q为直线外的一点,在直线上,为直线的方向向量,
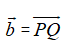
,则点Q到直线距离为
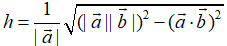
2.点到平面的距离若点P为平面外一点,点M为平面内任一点,平面的法向量为,则P到平面的距离就等于在法向量方向上的投影的绝对值.即
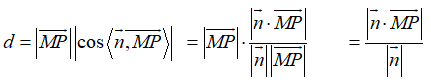
3.直线与平面之间的距离当一条直线和一个平面平行时,直线上的各点到平面的距离相等。由此可知,直线到平面的距离可转化为求直线上任一点到平面的距离,即转化为点面距离。即
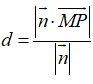
4.两平行平面之间的距离两平行平面间的距离处处相等,两平行平面间的距离转化为求点面距离。即
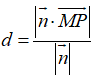
5.异面直线间的距离设向量与两异面直线都垂直,则两异面直线间的距离就是在向量方向上投影的绝对值。即








