
矩阵是一个非常重要的工具,它可以应用于数学的许多不同领域。在这里,我们将学习使用它们来解决常微分方程组(ODEs)。我们的方法将使用矩阵的一些特殊对象,即特征值和特征向量。

- 常微分方程组
什么是矩阵?
维基百科说,
矩阵是一个矩形的数字、符号或表达式的数组或表格,按行列排列,用来表示数学对象或该对象的某种属性。
但我个人更喜欢把它们看作是一次解决许多小而复杂问题的工具。它们形式上是一种二维向量,并被几乎每个高等数学领域所使用。我的老师曾经告诉我,“你越早爱上矩阵,你就会越早爱上数学”,我认为这完美地概括了这一点。
特征值和特征向量
特征值和特征向量(Eigenvalues and Eigenvectors)这两个词源于德语单词eigen,意为特殊、具体或特征,这几乎就是它们的定义。它们是与特定矩阵相关的特殊数字或向量。它们是内在的值,可以计算并用来正确理解一个矩阵。特征向量在矩阵变换下保持相同的角度,而特征值定义了这些变换的比例因子。
要找到特征值,我们可以遵循一个有效的方法:将矩阵的行列式减去每个对角线元素的特征值,然后令结果为零。对于二阶矩阵,这种方法会得到一个二次方程,可以通过因式分解解出,或者你也可以应用二次方程公式来解。特征值通常用希腊字母λ(lambda)来表示。


为了找到特征向量,我们可以直接使用其定义来计算。注意,对于矩阵的每个特征值,将有无限多的特征向量族。



这样我们就可以找到两个特征向量。个人来说,我喜欢设定a为1,并找到一个适合它的b。

解常微分方程组
首先,将常微分方程组转化为矩阵方程。

现在,我们可以确定解题步骤,因为这只是一个基本的指数微分方程,其解如下所示:

如果这个步骤不是很直观,那么我建议为每个对象替换变量,然后尝试解它,记住我们的参数是't'。
从这里开始,我们所需要做的就是计算这个矩阵的指数,我们可以使用一种叫做对角化的技巧来完成,结合我们之前找到的特征值和特征向量。
对角化
对角化过程涉及到将一个复杂的矩阵分解成三个相乘的更简单的矩阵,使得原始矩阵的特性和操作更易于处理。在这种情况下:
第一个矩阵,命名为 T:

这个矩阵是由原始矩阵的特征向量构成的。在这里,每个特征向量占据矩阵的一列。这样构造的矩阵 'T' 能够将原始矩阵通过一个线性变换带到一个更简单的形式,即对角矩阵。
第二个是在对角线上填充特征值,其他地方为0,我将其命名为D

最后一个是T的逆矩阵,我们可以使用二阶矩阵逆规则来计算,得到:

使用这三个矩阵,我们可以计算任何“解析”函数,比如指数函数或幂函数。现在,对这三个相乘的矩阵进行函数操作时,就得到:

由于对角矩阵,任何函数都可以化成单独的项,我们现在可以解决问题了。

从这里开始,我们所要做的就是将三个矩阵相乘,得到:

使用这个,我们可以得到y和x的两个方程:
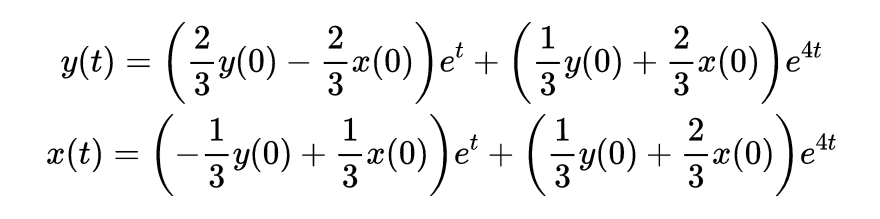
如你所见,矩阵是数学的一个基本领域,虽然一开始可能看起来难以应用,但它们实际上非常有用。矩阵教会我们要拓宽视野,不仅要关注直接问题,还要考虑更广泛的背景和细节,这样我们才能更全面地解决问题。如果你觉得这个观点启发了你,可以尝试通过更改原始方程中的数值来亲自解决类似的问题,这将帮助你更深入地理解矩阵的作用和应用。







